В последната си книга "В търсене на неизвестното: 17 уравнения, които промениха света“ (In Pursuit of the Unknown: 17 Equations That Changed the World) британският математик Иън Стюърд прави обзор на някои от най-важните математически уравнения в историята на човечеството.

Част от тях описват законите на физиката и водят до небивал технологичен разцвет. Други пък дефинират взаимовръзките в социалната сфера и икономиката, а трети управляват дигиталната революция, на която сме свидетели през последните десетилетия.

В следващите редове ви представяме 8 от тези уравнения, „участващи“ в живота ни буквално всеки ден.

1. Питагоровата теорема

Какво означава? Квадратът на хипотенузата на правоъгълен триъгълник е равен на сбора от квадратите на страните му

История: Макар че носи името на древногръцкия математик Питагор, не е сигурно, че той е бил първият, който я е доказал. Първото свидетелство за доказването на теоремата идва от Евклид (създателят на класическата евклидова геометрия). Част от историците на науката вярват, че първото доказателство на теоремата е било направено още от вавилонците хиляда години преди Питагор.

Важност: Питагоровата теорема е в основата на класическата геометрия. Освен това тя е една от връзките на геометрията с алгебрата и определя развитието на тригонометрията. Без това просто наглед уравнение развитието на навигацията и създаването на точни географски карти би било невъзможно.

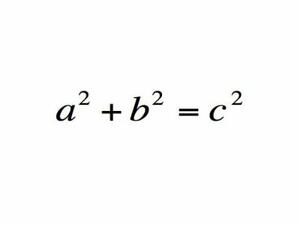Снимка: "Бизнес инсайдър"

2. Логаритъмът и неговите превъплъщения

Какво означава? Най-общо казано логаритъмът е такова число, което когато бъде използвано като степен на друго число, се получава трето, определено число.

История: Първоначалната концепция е била открита от шотландския математик Джон Непер в опитите му да улесни умножаването на големи числа, което по онова време отнемало много време и енергия. По-късно методът бил усъвършенстван от Хенри Бригс, който създал референтните логаритмични таблици.

Важност: Логаритмите довели до революция в изчисленията, улеснявайки неимоверно работата на инженери и астрономи. Макар че днес тази работа се върши от компютрите, логаритмите все още определят разбирането ни за радиоактивния разпад на химичните елементи.

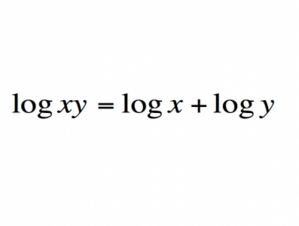
Снимка: "Бизнес инсайдър"

3. Законът на Нютон за гравитацията

Какво означава? С него се изчислява силата на гравитацията, която действа между две тела с определени маси, разположени на определено разстояние едно от друго.

История: Законът е изведен от британския учен сър Исак Нютон, който използвал по-ранните работи на немския астроном и математик Йохан Кеплер. Съществуват някои съмнения, че в работата си Нютон е плагиатствал от разработките на английския учен и негов съвременник Робърт Хук.

Важност: Законът се използва за описване на гравитационните взаимодействия между телата и на небесната механика. Макар че впоследствие той е обхванат от по-обширната Обща теория на относителността (ОТО) на Алберт Айнщайн, законът на Нютон продължава да върши отлична работа при практически задачи като определяне на траекторията на астероиди и изпращането на сателити в Космоса. Благодарение на него днес разполагаме с глобалните сателитни комуникации и сме успели да пратим хора в Космоса.

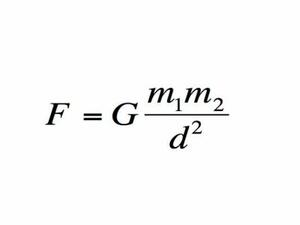
Снимка: "Бизнес инсайдър"

4. Нормалното разпределение

Какво означава? Тази формула определя стандартното нормално разпределение – крива с формата на камбана, която ни казва каква е вероятността да наблюдаваме дадено събитие.

История: Първоначалната работа по извеждането на формулата е дело на френския математик Блез Паскал, но самото нормално разпределение е открито от швейцареца Якоб Бернули. Познатата крива е изведена графично от белгийския математик Адолф Кетле.

Важност: Уравнението стои в основата на модерната статистика. Без него в сегашната си форма не биха могли да съществуват нито точните, нито хуманитарните науки. Днес формулата се използва например за определянето на ефективността на дадено ново лекарство.

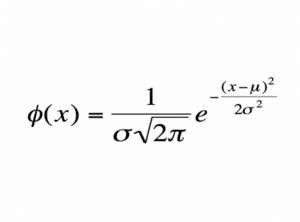
Снимка: "Бизнес инсайдър"

5. Вълновото уравнение

Какво означава? Диференциално уравнение, което описва поведението на различните видове вълни.

История: Описано за първи път от шведския математик Даниел Бернули и френския му колега Жан Д'Аламбер през 18-ти век.

Важност: Поведението на вълните обрисува начините, по които се разпространява звукът, по които се случват земетресенията, както и поведението на големите океански водни маси. В практиката законът се използва от петролните компании, които търсят нефт с помощта на експлозиви, предизвикващи специфични вълни в земните маси.

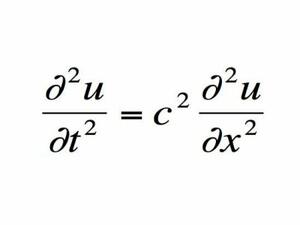
Снимка: "Бизнес инсайдър"

6. Уравненията на Максуел

Какво означават? Серия от четири уравнения, обединяващи явленията електричество и магнетизъм в обща теоретична рамка.

История: Първоначално по темата работи американският физик-изпитател Майкъл Фарадей. Неговите опити са описани по математически път от шотландеца Джеймс Максуел, като популярният им съкратен вид е изработен по-късно от немския физик Хайнрих Херц.

Важност: На тези уравнения се крепят много от технологиите, които приемаме за неделима част от живота си – радара, радиото, телевизията и модерните комуникации като цяло.

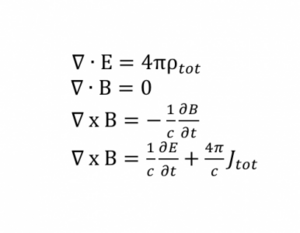
Снимка: "Бизнес инсайдър"

7. Уравнението на Айнщайн, обвързващо маса и енергия

Какво означава? Оказва се, че енергията, която даден физически обект съдържа в себе си, е равна на масата му, умножена по скоростта на светлината на квадрат.

История: До уравнението си Алберт Айнщайн достига след като анализира експеримент, проведен от Алберт Микелсън и Едуард Морли, с който двамата доказват, че светлината не се движи по правилата на нютоновата механика. Идеята е развита от Айнщайн в неговите Специална и Обща теории на относителността.

Важност: Вероятно най-важното уравнение в историята, което напълно променя възгледите ни за материята и реалността. То задава теоретичната рамка, водеща както до създаването на ядрените оръжия, така и до далеч по-“мирни“ технологии като GPS системите.

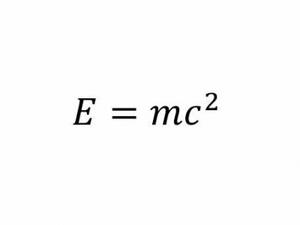
Снимка: "Бизнес инсайдър"

8. Уравнението на Google

В това уравнение се крие силата на световната интернет търсачка Google. По същество то показва как можем да използваме гимназиалната алгебра по умен начин, за да подредим резултатите при търсене в мрежата. Макар че то не е включено в книгата на Стюърд, авторът ѝ смята, че уравнение то има заслужено място в нея.

Снимка: "Бизнес инсайдър"

Тази статия ви хареса? Присъединете се към Еcon.bg и във Facebook, за да следите всичко най-интересно за икономиката, предприемачеството, кариерата, личните финанси, политиката и обществото!